4.1. LA DIMENSIÓN TEMPORAL DE LAS PREFERENCIAS Y LA NECESIDAD DE DESCONTAR
Hasta aquí hemos estudiado cómo deben estimarse tanto los costes como los resultados de los programas sanitarios para poder ser comparados entre sí. Implícitamente hemos supuesto que dichos costes y resultados acontecen en el mismo periodo de tiempo. Este supuesto, sin embargo, con frecuencia no es realista, ya que costes y resultados no suelen distribuirse de modo uniforme a lo largo del tiempo. Es plausible imaginar tres programas de oxigenoterapia que consumen recursos por un valor total de 6.000 euros durante los próximos seis años, produciendo los tres idéntico beneficio, pero incurriendo los costes en años diferentes. Supongamos que el programa A consume el 90 por 100 del valor mencionado en el primer año, distribuyendo el 10 por 100 restante de manera proporcional a lo largo de los cinco años restantes; con el programa B sucede al contrario: consume el 90 por 100 en el sexto año, repartiéndose el 10 por 100 restante entre los cinco primeros años; el programa C, en cambio, sí que distribuye los costes de manera uniforme durante los seis años: la misma cantidad cada año. Puesto que costes y beneficios totales son idénticos en los tres programas, ¿significaría eso que debería darnos igual financiar uno que otro?
La evaluación económica contesta negativamente a la anterior pregunta. La razón de esta negativa descansa sobre el argumento de la preferencia temporal. Al igual que la mayoría de las personas contratan seguros porque prefieren no correr riesgos, también la mayoría de las personas poseen una preferencia genuina por el momento del tiempo en que ocurren los costes e incluso los beneficios. En lo que concierne a los costes, la preferencia temporal de la mayoría de la gente parece caracterizarse por la paciencia –no se tiene prisa por pagar– mientras que cuando se trata de beneficios entonces se caracteriza por la impaciencia, ya que casi todo el mundo prefiere cobrar lo antes posible. En ambos casos decimos que se está descontando el futuro, ya que tanto el deseo de retrasar lo más posible los costes como la impaciencia por percibir lo antes posible los beneficios implica valorar más el consumo presente que el consumo futuro, de modo que 1 euro hoy vale más (se prefiere más intensamente) que 1 euro dentro de un año.
El mecanismo del tipo de interés de mercado puede concebirse como una expresión de la preferencia temporal que sirve para ilustrar la necesidad de descontar el flujo futuro de costes y beneficios de cualquier inversión. Es fácil advertir que 1 euro invertido en el presente a un tipo de interés del 3 por 100 será equivalente a 1,03 euros dentro de un año. Sin embargo, ¿cuál será el valor que tiene en el presente (VP) 1 euro de dentro de un año? Parece evidente que la respuesta a esta pregunta vendrá dada por la resolución de la igualdad VP × 1,03 = 1 euro. Por tanto, VP = 1/1,03 = 0,97 euros. En efecto, parece que 1 euro hoy vale más que 1 euro dentro de un año, ya que recibimos un premio de 3 céntimos por posponer el consumo en un año, del mismo modo que la suma equivalente en el presente a recibir 1 euro dentro de un año es 3 céntimos menor. Por consiguiente, si queremos comparar costes y beneficios que tienen lugar en distintos momentos del tiempo hemos de convertir todos sus valores futuros en su valor equivalente en el momento actual. El procedimiento aritmético que permite esa conversión es lo que denominamos descuento.
Antes de aplicar el procedimiento del descuento a los programas sanitarios hay que reparar en la naturaleza heterogénea de los resultados de salud. El ejemplo que acabamos de ver ilustra de forma muy simplificada la necesidad de descontar los costes futuros, ya que éstos se expresan en unidades monetarias. Sobre este punto no parece haber ningún tipo de controversia entre los estudiosos de la evaluación económica. Este consenso incluso podría extenderse a los resultados monetizados en el marco del ACB, pero ¿qué decir del resto de análisis en los que se utilizan unidades como las vidas salvadas o los AVAC? Resulta evidente que no existe un «banco» para este tipo de resultados, ni tampoco existe un tipo de interés que demuestre las diferencias entre el valor presente y el valor futuro. Aquí sí surge la controversia. Por esta razón, dejaremos para más adelante el problema del descuento de los resultados, haciendo ahora referencia únicamente al descuento de los costes.
La aplicación del procedimiento del descuento al flujo futuro de costes asociados a un programa sanitario se calcularía del siguiente modo:
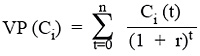
donde VP (Ci) es el valor presente de los costes del programa i, Ci (t) representa los costes del programa i en el periodo t, r es la tasa de descuento, y n la duración total del proyecto.
La tasa de descuento r no es más que la cuantificación de la preferencia temporal, lo que a nivel individual coincide con el tipo de interés (el 3% del ejemplo anterior). Ya que la tasa de descuento es mayor que cero, suele decirse que la preferencia temporal es positiva. Puede comprobarse fácilmente que el valor presente de cualquier cantidad futura será tanto menor cuanto mayor sea la tasa de descuento y/o más distante esté del presente el momento futuro en que se consume.
La anterior expresión supone que todos los costes tienen lugar al comienzo de cada año. Este supuesto no es irrelevante, por cuanto el coste correspondiente al primer periodo (t = 0) no se descontará. Si, en cambio, los costes tienen lugar al término de cada año, entonces el valor presente del coste del año inicial sí tendría que descontarse porque coincidiría con el comienzo del año 1. Esto requeriría simplemente iniciar el sumatorio de la fórmula del valor presente en t = 1.
4.2. LA ELECCIÓN DE LA TASA DE DESCUENTO
Hemos afirmado en el anterior epígrafe que la tasa de descuento individual equivaldría al tipo de interés de mercado. Sin embargo, es sencillo constatar que existe un amplio abanico de diferentes tipos de interés de mercado (por ejemplo, el de la deuda pública, el de los depósitos bancarios, el de los fondos de inversión, etc.), así que incluso en el caso de las decisiones estrictamente individuales la elección de la tasa de descuento es un asunto complicado. Sólo en el caso ideal (y por tanto irreal) en que la economía funcionase de forma perfecta (por ejemplo, no hubiera monopolios ni oligopolios) habría un único tipo de interés, el cual serviría tanto para las decisiones individuales (por ejemplo, ahorrar) como para las decisiones colectivas (por ejemplo, asignar recursos presupuestarios entre diferentes programas sanitarios) 22. Como está claro que esta situación no se da en la práctica, ¿qué tasa de descuento se debería utilizar para descontar los costes de los programas sanitarios?
Con el paso del tiempo se han llegado a dibujar en el plano teórico dos posturas respecto de la elección de la tasa social de descuento que debe aplicarse a cualquier programa o inversión pública:
- El denominado enfoque del coste social de oportunidad, según el cual la tasa social de descuento sería un promedio ponderado de las tasas de rendimiento reales de la inversión privada de aquellos sectores de la economía que se ven desplazados por la financiación de los programas públicos.
- El denominado enfoque de la tasa social de preferencia temporal, que afirma que el auténtico coste de oportunidad de los programas públicos vendría dado por la tasa de rendimiento real de las inversiones sin riesgo. Esto representa equiparar la tasa social de preferencia temporal al tipo de interés real de la deuda a largo plazo.
Al margen de planteamientos teóricos, lo cierto es que la evaluación económica no permanece inactiva, aplicando un rango de valores para la tasa de descuento que ha ido variando con el paso del tiempo. Hace dos décadas se llegaban a aplicar tasas de descuento incluso del 10 por 100, sin embargo de forma pareja al descenso de los tipos de interés reales, también han ido reduciéndose los valores recomendados por las agencias públicas de evaluación económica. En la actualidad, podría decirse que el rango más frecuente de valores se sitúa en el intervalo 3-5 por 100, llegando a aplicarse incluso valores por debajo del 3 por 100. Así, por ejemplo, la Oficina de Gestión y Presupuesto estadounidense recomienda en una guía publicada en 2003 descontar costes y beneficios a una tasa comprendida entre el 1 por 100 y el 5 por 100.
4.3. ¿CÓMO SE DEBEN DESCONTAR LOS RESULTADOS?
Hay autores (por ejemplo, Brock, 1998) que platean objeciones éticas a descontar los resultados de los programas sanitarios, ya que afirman que hay intervenciones sanitarias que mejoran la salud al cabo de años, de manera que si esos beneficios se descuentan de forma inadecuada, habría programas sanitarios potencialmente muy valiosos que quedarían relegados a favor de aquellos otros que producen los resultados de una forma inmediata. El descuento podría así discriminar a generaciones futuras respecto de generaciones actuales, que no invertirían dinero suficiente en programas que, por ejemplo, mejoren las expectativas de vida de los neonatos. Otro tipo de objeciones de índole descriptiva y no normativa se basarían en la evidencia encontrada por algunos investigadores (por ejemplo, Cairns y van der Pol, 1997) que parece sugerir que no todas las personas poseen una preferencia temporal positiva, de forma que hay gente que prefiere recibir los beneficios cuanto más tarde mejor.
Existen, sin embargo, contra-argumentos a favor no sólo de descontar los resultados de los programas sanitarios, sino también de aplicar la misma tasa de descuento que se aplique a los costes. En concreto, se destacan en la literatura científica dos «pruebas» de la necesidad de descontar los beneficios sanitarios, la paradoja de Keeler-Cretin y el argumento de consistencia de Weinstein y Stason 23.
La paradoja de Keeler-Cretin consiste en que si los costes de un programa son descontados, mientras que los resultados no lo son, o lo son a una tasa inferior, siempre es posible incrementar la razón coste-efectividad del programa (efecto por unidad monetaria gastada) simplemente retrasando su inicio. La implicación de este resultado es que nunca se llevaría a cabo el programa, posponiéndose indefinidamente.
El argumento de consistencia de Weinstein y Stason sostiene que la razón fundamental por la que deben ser descontados los resultados futuros es porque la evaluación económica compara los resultados sanitarios con el dinero que cuesta obtenerlos. Si admitimos que esa relación es estable en el tiempo, entonces el descuento de los costes impele al descuento de los resultados futuros, o de lo contrario se estaría siendo incosistente, ya que de hecho cada euro futuro se descuenta en relación a cada euro presente. Asimismo, la consistencia exige que la tasa de descuento que se aplique sea idéntica a la de los costes.
En conclusión, si bien el descuento de los beneficios a una misma tasa que los costes no es una práctica universal 24, ya que hay algunos países que no descuentan los resultados o lo hacen a una tasa menor que la de los costes, sí suele ser la práctica general recomendada entre otros por el Panel de Expertos sobre Coste-Efectividad en Salud y Medicina.
Por tanto, el descuento de los resultados de un programa sanitario se haría aplicando la misma fórmula que antes utilizábamos para los costes, sólo que ahora obviamente las medidas de resultados y no los costes ocuparían el numerador. Tendríamos:
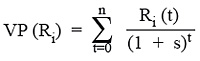
donde VP (Ri) es el valor presente de los resultados del programa i, Ri (t) representa los resultados del programa i en el periodo t, s es la tasa de descuento, y n la duración total del proyecto.
A consecuencia de que convenimos que la tasa de descuento de los resultados debe coincidir con la tasa de descuento de los costes, entonces s = r. Por lo demás, el significado e interpretación de los elementos de esta fórmula es idéntico a la de los costes, siendo también de aplicación aquí las mismas salvedades que hacíamos antes para los costes respecto del momento inicial o final del año en que tienen lugar.
4.4. INCORPORACIÓN DE LA INCERTIDUMBRE AL ESTUDIO DE EVALUACIÓN
El cálculo de los costes y beneficios de los programas sanitarios, así como su integración en un modelo de toma de decisiones como los que pueden apreciarse en varios de los casos que ilustran los contenidos del capítulo, está sujeta a incertidumbre.
La fuente más evidente de incertidumbre es la que rodea a los parámetros (por ejemplo, probabilidad de éxito del tratamiento) que se requieren para estimar los costes y beneficios. Dicha incertidumbre puede provenir de la falta de datos en los que basar el valor del parámetro, de la difícil extrapolación de las estimaciones obtenidas de una muestra específica a la población objetivo del estudio, o de la falta de consenso teórico acerca de cómo estimar el parámetro.
Asimismo, los datos sobre costes y beneficios se combinan en un modelo de acuerdo a ciertos supuestos estructurales que también están expuestos a incertidumbre. Éste es el caso, por ejemplo, del criterio seguido para manejar en el análisis el hecho de que una enfermedad se caracterice por su recurrencia, pese al tratamiento aplicado inicialmente. La incorporación de esta característica requiere adoptar una visión dinámica sujeta a supuestos muy restrictivos, que deben hacerse explícitos en el estudio.
En general, hay dos formas de afrontar el problema que representa la incertidumbre sobre los parámetros en los ejercicios de evaluación económica:
- Realizar análisis de sensibilidad que verifican la robustez de los resultados del análisis introduciendo pequeñas modificaciones en los valores de los parámetros.
- Utilizar métodos estadísticos que estiman una distribución de probabilidad para los valores de los parámetros inciertos, con el fin de elaborar regiones de confianza.
El análisis de sensibilidad más frecuente es el análisis de una variable o univariante, en el que se modifica el valor de uno de los parámetros, mientras el resto de las variables se mantienen inalteradas. A continuación, se verifica si la estrategia óptima cambia o no, según lo hagan los valores del parámetro seleccionado. Aunque este tipo de análisis de sensibilidad es el más sencillo, no es el más correcto, dado que los parámetros en realidad no suelen ser independientes unos de otros. Por ejemplo, si modificamos la probabilidad de sufrir efectos adversos, esto repercutirá sobre los costes de los tratamientos necesarios para atender ese tipo de complicaciones. Si sólo recogemos la variación en la probabilidad, y no su transmisión a los costes, estaremos infravalorando la variabilidad en la ratio coste-resultado final, sesgando de esta forma las conclusiones del análisis.
Como respuesta a las limitaciones del análisis univariado existe la posibilidad de hacer análisis más complejos, en los cuales se pueden modificar simultáneamente dos, tres o más parámetros. Ésta es la esencia del análisis de sensibilidad multivariante. Su principal inconveniente radica precisamente en su mayor complejidad, lo que puede convertirlo en inmanejable si el número de parámetros involucrado es muy grande.
En el siguiente recuadro se ilustra con un estudio empírico la aplicación de otro tipo de análisis de sensibilidad conocido como análisis de umbral, el cual sirve para identificar el valor crítico de un parámetro clave para la decisión que se está analizando.
|
RECUADRO 11. Análisis de umbral para programas de prevención del VIH (Holtgrave y Qualls, 1995). Introducción. Existe un importante número de evaluaciones económicas relacionadas con los tratamientos para la infección del VIH, pero no con las actividades voluntarias de prevención del contagio (por ejemplo, uso del condón). En parte, esta ausencia de trabajos se debe a la incertidumbre que rodea a muchos de los elementos a tener en cuenta (por ejemplo, cambios en los hábitos de comportamiento) para evaluar correctamente la efectividad de las medidas de prevención. Este estudio utiliza el enfoque del análisis de umbral para intentar paliar dicha incertidumbre. Objetivos. Se plantean dos objetivos: 1. Estimar el umbral monetario por encima del cual la sociedad probablemente no estaría dispuesta a pagar por evitar una infección por VIH; 2. Analizar la sensibilidad del umbral ante cambios en los valores de base de los parámetros. Métodos. El tipo de evaluación económica escogido es el ACU, empleando los AVAC como medida de resultados. La perspectiva seleccionada es la social. El curso vital de un infectado tipo se divide en cuatro etapas de distinta duración y calidad de vida. Se considera una esperanza de vida de 65 años, suponiéndose inicialmente que el paciente muere a los 38 años (pierde 27 años potenciales de vida). Todos los datos sobre duración, utilidad de la calidad de vida, así como la DAP por AVAC ganado provienen de la literatura. La tasa de descuento inicial fue del 5 por 100. Los autores calculan la diferencia entre los AVAC de una persona sana y los AVAC de una persona infectada, multiplicando esta diferencia por la DAP por AVAC ganado, descontándolo todo al 5 por 100. El valor resultante es el umbral monetario por encima del cual no se estaría dispuesto a pagar por evitar una infección de VIH. Tabla 5. Resultados del análisis de sensibilidad
Resultados. El umbral se estima inicialmente en 417.000 dólares (dólares de 1993) por infección de VIH evitada. En la tabla 5 podemos apreciar el gran efecto que tiene sobre la magnitud del umbral variar dos de los parámetros del modelo, la DAP por AVAC ganado y el número potencial de años perdido. |
En cuanto a los métodos estadísticos disponibles para el tratamiento de la incertidumbre, pueden elaborarse regiones de confianza de varias maneras 25, cuyo estudio excede las pretensiones de este capítulo. Aclaremos, no obstante, que el término región de confianza no es sino una generalización del concepto estadístico de intervalo de confianza. Un intervalo de confianza es el rango de valores entre los cuales podemos confiar en encontrar el verdadero valor del parámetro con probabilidad elevada (por lo general el 95%). En el caso de la evaluación económica hablamos de la región en que confiamos se encuentre el verdadero valor de la ratio coste-resultado.
22 Una amplia discusión sobre este punto puede encontrarse en las páginas 216-217 de Gold et al., (1996).
23 Keeler y Cretin (1983), Weinstein y Stason (1977).
24 Sirvan como ejemplo los cambios ocurridos en esta materia recientemente en dos países europeos: el Reino Unido y los Países Bajos. Hasta el año 2003 en el primero de ellos se recomendaba el uso de una tasa del 6 por 100 para descontar los costes y otra del 1,5 por 100 para descontar los efectos; desde dicho año se recomienda el uso de una misma tasa del 3,5 por 100 para ambos. En los Países Bajos el cambio ha operado en sentido inverso: de proponerse una tasa de descuento común del 4 por 100 para costes y efectos, se ha pasado a recomendar el uso de sendas tasas del 4 por 100 y el 1,5 por 100 para costes y resultados, respectivamente.
25 Análisis de bootstrap de datos procedentes de ensayos clínicos, enfoques bayesianos que combinan datos con distribuciones subjetivas, estimaciones paramétricas a partir de muestras empíricas, etc. Una descripción de varios de estos métodos puede encontrarse tanto en Gold et al., (1996) como en Drummond et al., (2005).



